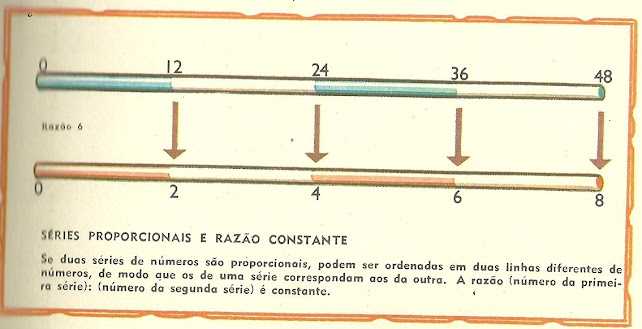
A série de números 12, 24, 36, 48 tem uma propriedade importante em comum com a série 2, 4, 6, 8: 12 é 2 vezes 6; 24 é 4 vezes 6; 36 é 6 vezes 6; 48 é 8 vezes 6.
Os números da primeira
série são 6 vezes maiores que os correspondentes da segunda série.
Outra forma de exprimir
isso é:
12/2 = 2; 24/4 = 6 e assim sucessivamente.
Isto é o que se chama razão ou relação: um número de uma série é comparado com o número
correspondente da outra. Se a razão de todos os pares de números que se
correspondem nas duas séries for a mesma, diz-se que as séries são proporcionais.
Na vida real há muitos
pares de quantidades que são proporcionais. Deixando-se ligada uma estufa durante
uma hora, talvez o custo de eletricidade consumida seja de 3 centavos (exemplo
hipotético). Nesse caso, ao fim de duas horas, será de 6 centavos.
O consumo de
eletricidade corresponde a uma série de números — 3, 6, 9, 12 —, e o tempo em
horas, a outra série: 1, 2, 3, 4.
A razão 3/1 é 3, a razão 6/2 é 3 e
assim sucessivamente.
IMAGEM 01 – RAZÕES E PROPORÇÕES
Portanto, as duas séries de números são proporcionais. É evidente que se as duas quantidades são proporcionais, uma delas será tanto maior quanto maior venha a ser a sua correspondente na outra série. Quanto mais tempo a estufa ficar ligada, maior será o custo de eletricidade consumida. O custo é proporcional ao tempo.
Outro exemplo é o do
homem andando a 4 quilômetros por hora. Mantendo-se a mesma cadência, a
distância percorrida será proporcional ao tempo. Ao fim da primeira hora terá
percorrido 4 quilômetros; ao fim da segunda, 8, e assim sucessivamente. As duas
quantidades — distância e tempo — correspondem a duas séries de números:
distância
em quilômetros 4 8
12 16
tempo
total em horas 1 2
3 4
Novamente é óbvio que a
distância é proporcional ao tempo. A razão da distância (em quilômetros) ao
tempo total (em horas), para os termos correspondentes, é sempre a mesma. Neste
exemplo é igual a 4.
IMAGEM 02 – AS RAZÕES E A LEI DE OHM
Quando se sabe que as duas
séries são proporcionais, é fácil achar um termo desconhecido de uma delas. Suponhamos
que o problema é determinar a distância percorrida em 6 horas. Podem ser usados
símbolos matemáticos. A distância desconhecida é representada pela incógnita x.
X deve pertencer à série
das distâncias. Pode ser relacionada com a série tempo, por meio de uma equação. Estes dados são suficientes
para determinar x.
A razão x/6
X = 4 x 6
(multiplicam-se os dois membros da equação por 6).
X = 24
A resposta do problema
é: a distância percorrida é 24 quilômetros.
As propriedades das
séries proporcionais podem ser representadas de outra maneira.
Aumentos iguais, nos
termos de uma série, correspondem a aumentos iguais nos termos da outra série. No
exemplo: 12, 24, 36, 48 —1, 2, 3, 4, aumentos iguais de 12 unidades, na
primeira série, correspondem a aumentos iguais de uma unidade na outra série. Esta
propriedade é melhor compreendida quando as duas séries são representadas num
gráfico.
IMAGEM 03 – GRÁFICO RAZÕES E PROPORÇÕES



Nenhum comentário:
Postar um comentário